О сочетании больших циклов
Оригинал — http://zmey.club/research/66-o-sochetanii-bolshih-ciklov.html
Как сочетаются большие циклы по разным активам? Какие из них двигаются синхронно, а какие живут исключительно своей жизнью? Правда ли, что золото всегда ходит против доллара, а фондовой рынок США растёт только в условиях недорогой нефти? Как правильно формировать стратегический портфель и как выбирать для него действительно недооценённые активы? Как сравнить активы с принципиально разными свойствами и будет ли такое сравнение честным?
Когда аналитики говорят о сравнении, то обычно подразумевают корреляцию, если вообще используют какие-то научные методы. Для примера, коэффициент корреляции между золотом и индексом доллара за последние 20 лет составляет порядка -0.4 (на дневных данных) — этого явно мало для формирования портфеля «без риска», но вполне достаточно, чтобы эксперты видели в них полную противоположность. Следующий пример показывает насколько опасна такая концепция.
Рассмотрим два циклических ценовых ряда, построенных согласно принципам Хёрста:
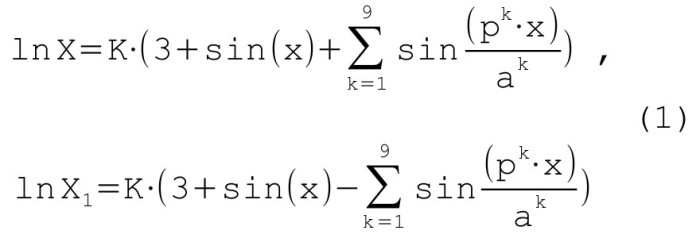
K=1, p=3.6, a=2
Как видно из формулы, слагаемые с наибольшим периодом софазны, тогда как все остальные торгуются чётко в противофазе. Периоды слагаемых попарно равны, а амплитуды снижаются вслед за периодом, хоть и не пропорциональны ему. Коэффициент корреляции в этой системе равен -0.98 (при разбиении интервала 0...2*Pi на 1000 элементарных отрезков), но это отнюдь не препятствие чтобы активы X и X1 глобально двигались вместе (рисунок 1), создавая ложное впечатление о своём характере.
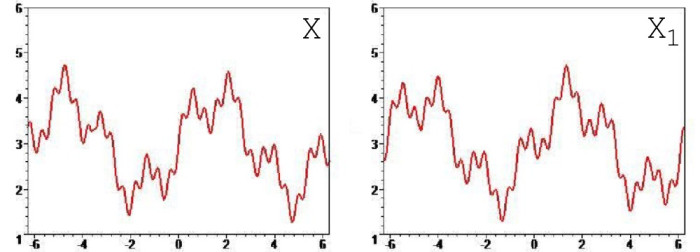
Рисунок 1 — графики X и X1 (показано только три слагаемых ряда)
В дальнейшем я покажу, что описанная мной картина является только чересчур идеализированной, но отнюдь не чисто гипотетической, а это, в свою очередь, ставит под сомнение многие хорошо известные закономерности, а заодно и подрывает основы всей построенной на корреляциях портфельной теории, ведь по правилам математической логики одного-единственного негативного результата достаточно для отрицания всей концепции. Разумеется, теорию нужно дополнять, но никак не отбрасывать.
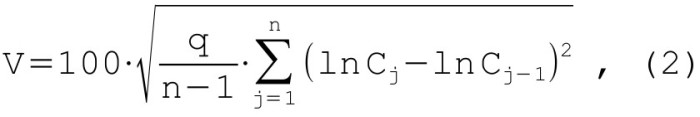
где Cj — цена закрытия рынка на баре с индексом j,
q — число наблюдений в году (для дневных данных q=252).
В традиционном понимании волатильность отвечает только за колебания рынка, но в действительности это интегральная характеристика, которая затрагивает и глобальные циклы, потому что все амплитуды обязательно связаны. Если одна из них отклонится от нормы, то на определённых тайм-фреймах станет выгодна систематическая игра или по тренду или против него, а это явное противоречие логике рынка, который не должен предоставлять трейдерам столь тривиальных возможностей.
Волатильность это объективная характеристика, которая, в отличии от всех амплитуд, рассчитывается непосредственно на основе ценовых данных с использованием простой и проверенной формулы. Кроме того, с графика чистого сентимента можно снять так называемую полную амплитуду А0, то есть разницу (в логарифмах) между вершиной и впадиной одного старшего цикла. Свяжем эти величины, используя их аналоги в рамках всё той же идеализированной циклической модели (формула 1):
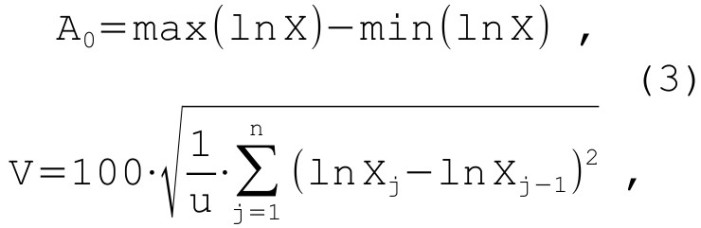
где u — период большого кондратьевского цикла.
Проведём численный эксперимент, чтобы установить, как именно те или иные переменные влияют на волатильность. Разобьём интервал 0...2*Pi на 10000 элементарных участков и зафиксируем значения p и a, после чего, варьируя коэффициентом K, будем добиваться изменения полной амплитуды. Построив график A0(V) (рисунок 2a) мы убедимся, что их взаимосвязь линейная (A0=U*V) и она остаётся таковой при любых значениях p и a, от которых зависит только лишь коэффициент U.
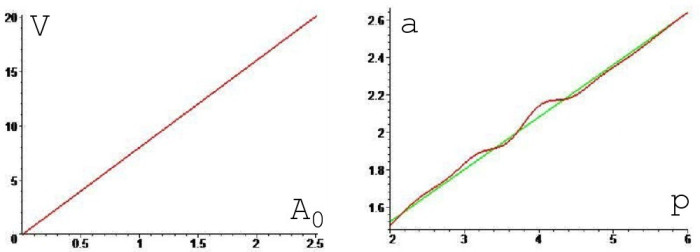
Рисунок 2a — взаимосвязь между волатильностью и полной амплитудой.
Рисунок 2b — взаимосвязь между амплитудой и периодом в идеальных циклах;
красная линия — экспериментальная, зелёная — приближение по формуле a=0.96+0.28p.
Значение коэффициента U=1/8 мы определим на основе реальных ценовых данных по шести наиболее ликвидным активам, предположив, что все они имеют одинаковый характерный период старшего цикла u=55 лет (таблица 1). Разброс полной амплитуды относительно её теоретического значения получается совсем небольшой, а это, в свою очередь, говорит не только об устойчивости найденного решения, но и также о фрактальном подобии графиков самых различных финансовых инструментов.
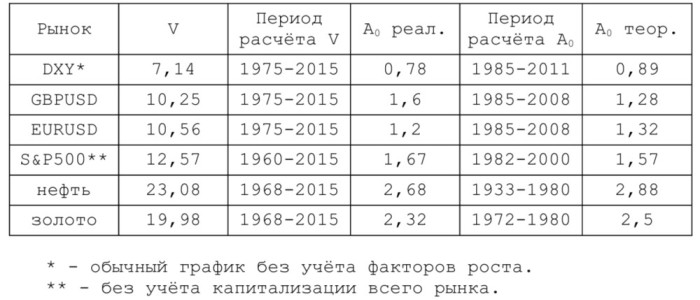
таблица 1 — волатильность и полная амплитуда по основным активам.
Напоследок мы решим обратную задачу, ради которой и затевался численный эксперимент — определим значения a и p, при которых коэффициент U = 1/8. Поскольку в нашей расчётной схеме неизвестных больше чем уравнений, то мы найдём только зависимость a(p), благо что она получается явной, то есть одному конкретному значению p соответствует одно конкретное значение a. Как видно из рисунка 2b, эта связь практически линейная, причём амплитуда убывает гораздо медленнее периода.
Рисунок 3 — исходные синусоидальные функции.
f1=3+sin(x),f2=3+sin(x+t).
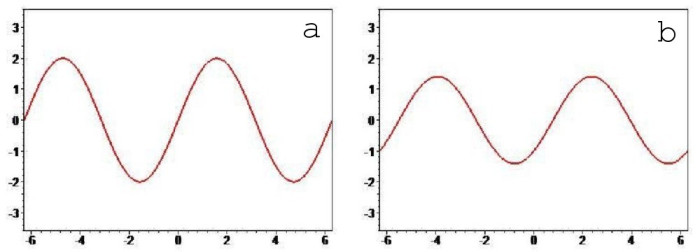
Рисунок 4 — отношение функций с одинаковым периодом.
a — активы f1 и f2 торгуются в противофазе (t=Pi),
b — общий случай, когда фазы не совпадают.
Очевидно, что период результирующей функции при таком раскладе всегда будет равен периодам двух исходных за исключением одного-единственного случая (t=0), когда f3 вырождается в прямую линию. Амплитуда f3 также зависит от величины t, достигая своего пика в противофазе (t=Pi). Циклы итоговой функции симметричны относительно вертикалей, проведённых через вершины, фаза равна -t/2.
Теперь усложним картину и представим, что каждая исходная функция является суммой двух синусоид, младшая из которых имеет реалистичную амплитуду, соразмерную своему периоду (рисунок 5).

Рисунок 5 — исходные функции, состоящие из двух синусоид.
f1=3+sin(x)+sin(px)/a; f2=3+sin(x+t1)+sin(px+t2)/a.
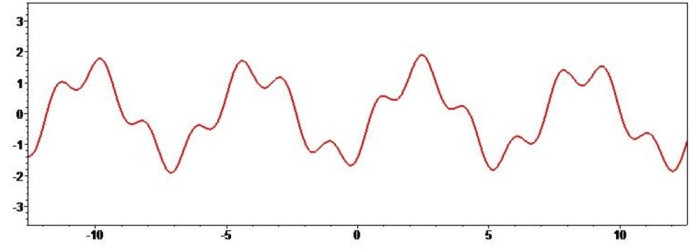
Рисунок 6 — отношение функций, состоящих из двух синусоид.
Параметры расчёта: p=3.6, a=2, t1=Pi/2, t2=Pi/3.
Как видно из рисунка 6, характерный период результирующей функции f3 по-прежнему равен 2*Pi, то есть глобальная циклическая картина определяется соотношением только первых слагаемых исходных функций, имеющих наибольшую амплитуду. Все остальные компоненты f1 и f2 влияют только на форму результирующей функции. Если младшие циклы находятся в противофазе, тогда перепады настроения на графике f3 получатся особенно резкими. Софазные младшие циклы взаимно уничтожаются.
Следующий пример, когда периоды старших циклов несколько отличаются, но их амплитуды абсолютно равны (рисунок 7). Периоды младших циклов пропорциональны старшим, фазы не имеют значения.
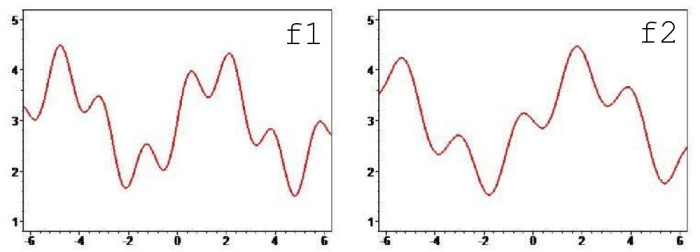
Рисунок 7 — исходные функции с разными периодами.
f1=3+sin(x)+sin(px)/a; f2=3+sin(qx)+sin(qpx+t)/a.
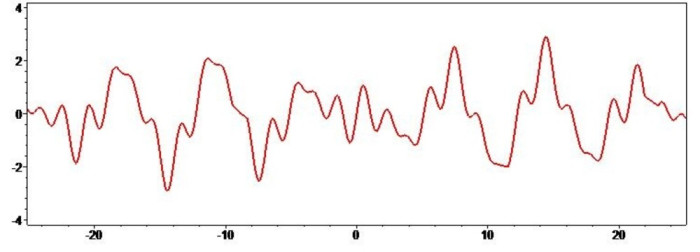
Рисунок 8 — отношение функций с разными периодами.
Параметры расчёта: p=3.6, a=2, q=3/4, t=Pi/2.
Рисунок 8 наглядно показывает что происходит с результирующей функцией f3, если исходные активы не связаны никакими взаимными обязательствами. В одной части графика может наблюдаться широкий диапазон с метаниями из стороны в сторону, но за ним неизбежно последуют несколько острых циклов, когда глобальные низы по одному активу начнут совпадать с верхами другого. Картинка при этом будет очень похожа на случай равных периодов в противофазе, но это не продлится долго.
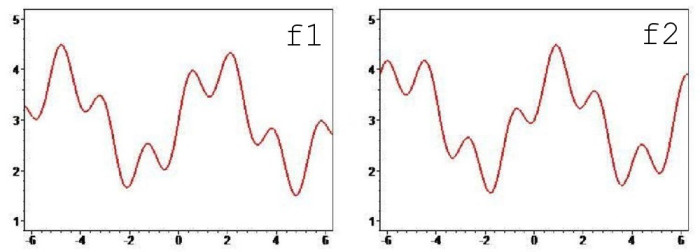
Рисунок 9 — исходные функции (старшие циклы софазны).
f1=3+sin(x)+sin(px)/a; f2=3+sin(x+t1)+sin(px+t2)/a.
Последняя реалистичная ситуация, когда старшие циклы исходных функций имеют равный период, но их фазы практически совпадают (рисунок 9). При вычитании подобные циклы взаимно уничтожаются, оставляя после себя колебания с периодом 2*Pi/p (рисунок 10), зато при сложении они отлично видны (рисунок 11). Средний период по-прежнему равен 2*Pi, а вот полная амплитуда, если младшие циклы в противофазе, может оказаться практически равной амплитуде на рисунке 10.
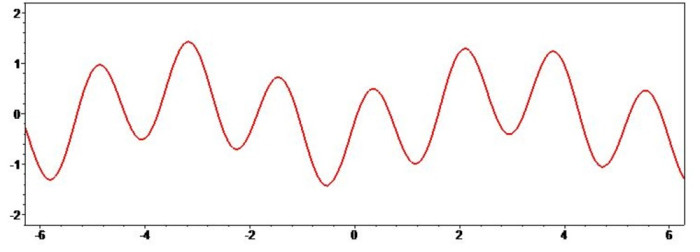
Рисунок 10 — вычитание функций (старшие циклы софазны)
Параметры расчёта: p=3.6, a=2, t1=Pi/6, t2=-3*Pi/4.
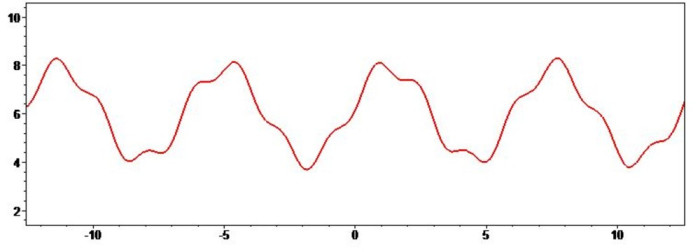
Рисунок 11 — сложение функций (старшие циклы софазны).
Параметры расчёта: p=3.6, a=2, t1=Pi/6, t2=-3*Pi/4.
Очевидно, что полная независимость каких-то активов это чисто гипотетический случай, потому что все они связаны через инфляцию, которая является такой же циклической функцией. Нам должно выбрать — либо все активы имеют одинаковый характерный период, равный периоду цикла Кондратьева, либо в один прекрасный момент на пике инфляции мы получим низкие процентные ставки, недорогое сырьё и пузырь на фондовом рынке. Логика ценообразования подсказывает, что выбирать нужно первое.
Получается, что всё многообразие вариантов, по сути, сводится только к рассмотрению фазы. При этом, имея даже сравнительно небольшую историю (примерно 60 лет), на основе результирующей функции можно однозначно определить все свойства исходных. Если периодично соотношение котировок, тогда исходные активы имеют разную фазу, если периодично произведение, тогда фазы должны совпадать. Таким образом, для выявления циклических свойств не нужно делать никаких вычислений!
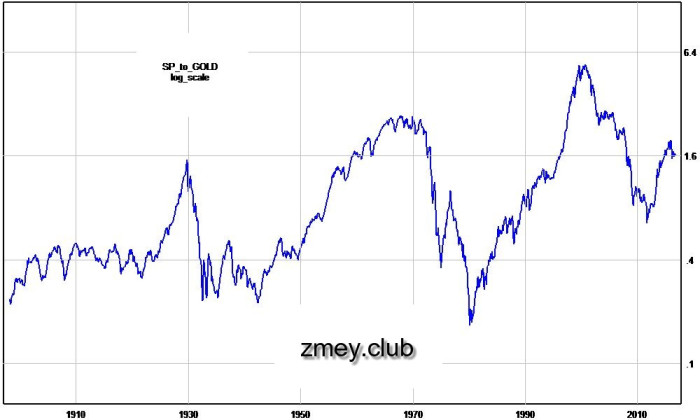
Рисунок 12 — отношение индекса S&P500 к золоту.
На рисунке 12 показано отношение индекса S&P500 к золоту — периодическая картина здесь аккуратно повторяет циклы Кондратьева по самому рынку Соединённых Штатов, а глобальные волны не содержат никакого постороннего шума. Нет сомнений, что эти активы циклически связаны, причём торгуются они практически в противофазе. Старшие верхи по индексу S&P совпадают с низами по золоту и наоборот; по времени разница между точками разворота составляет не больше 5 лет.
Безусловно, твёрдые котировки золота до начала 70-х годов наложили свой отпечаток на график, но их влияние лучше всего заметно как раз там, где циклическая картина содержит какие-то искажения — это болтанка 33-го года и слишком мелкая впадина в начале 40-х. Ранее 1920-го года наш график и вовсе не показателен, поскольку индекс S&P в те времена никак не отражал динамику капитализации рынка. Это тот случай, когда влияние факторов роста нельзя считать консервативным.
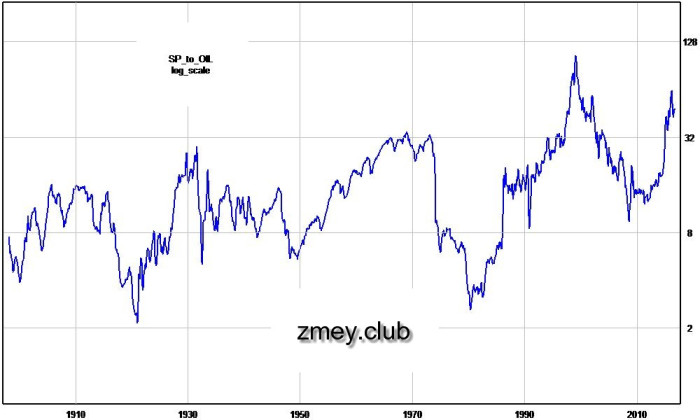
Рисунок 13 — отношение индекса S&P500 к нефти.
На рисунке 13 показано отношение индекса S&P500 к нефти — и циклы здесь тоже видны. Они не столь безупречны в плане шума, но такая картина указывает лишь на различную природу ценообразования. Для золота, валюты и фондовых рынков фактором роста является денежная масса, для нефти — только инфляция. Эти величины связаны между собой циклически, но никакой функциональной зависимости между ними, разумеется, нет — это и приводит к «потрясениям» на графике.
Сравнение чистых сентиментов (рисунок 14) позволяет нам получить более совершенную циклическую картину. Как и положено, график теперь развивается в горизонтальном канале, а чрезмерный рост с 2014-го года отлично укладывается в рамки коррекции, необходимой для растягивания цикла вправо. Волатильность нефти и наличие длительных периодов дисбаланса спроса и предложения по-прежнему напоминают о себе, но положения главных вершин и впадин они не меняют.
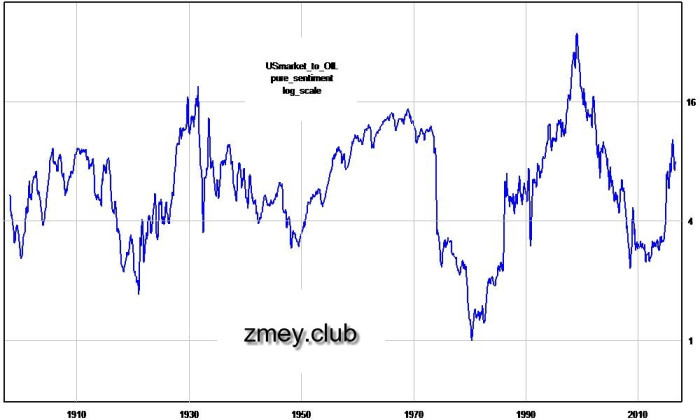
Рисунок 14 — отношение рынка акций США к нефти (чистый сентимент).
На протяжении всего XX века ключевые низы по американскому рынку с точностью до нескольких лет совпадали с верхами по нефти, если считать их в постоянных долларах — так было в 1921-ом, 1949-ом, 1982-ом и 2008-ом годах. При этом на истории хватает примеров, когда нефть и фондовый рынок США годами уверенно двигались в одну сторону, но это случалось исключительно по вине младших циклов, которые в случае с нефтью имеют запредельную и нестабильную амплитуду.
Годы Великой Депрессии проясняют нам некоторые особенности ценообразования нефти и золота. Так, падение рынка с 1929-го по 1932-ой годы проходило в условиях резкого увеличения спроса на золото, что в итоге привело к повышению его официального курса, тогда как нефть, следуя в русле дефляции, продолжала своё падение вплоть до 1933-го года. Тем не менее, к 1949-му году, когда американский рынок достиг существенной впадины, нефть догнала золото и также установила вершину.

Рисунок 15 — отношение золота к нефти.
Отдельно отмечу, что исследование циклических свойств требует особой тщательности и всестороннего анализа фактов. Так, рассматривая график отношения золота к нефти (рисунок 15) мы запросто могли обмануться, предположив их разную периодичность. Картина прояснилась только при их сравнении с индексом S&P500 — несмотря на различную природу факторов роста глобально нефть и золото всё-таки ходят вместе, как того требует логика инфляционных циклов.
По сути, наша задача заключается в том, чтобы придумать аналог исходного графика, на котором будут сохранены все базовые пропорции, но волатильность и, как следствие, полная амплитуда цикла станут равными соответствующим показателям другого актива. Логически это означает, что разницы котировок между двумя произвольными барами на основном графике и на его аналоге всегда отличаются ровно в u раз. Отсюда, массив данных для построения графика-аналога определяется формулой:
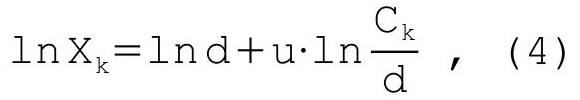
где Сk — исходная котировка на баре с индексом k,
d — любое положительное число (d>0).
Коэффициент u равен отношению волатильностей двух сопоставляемых активов, так что весь принцип, согласно которому один из них растягивается по вертикали, можно смело назвать паритетом величины V. Параметр d в данном случае просто число, прибавленное к функции, — оно определяет номинальную котировку, но никак не влияет на логарифмические пропорции. Исходный график по индексу доллара представлен на рисунке 16, а его аналог с амплитудой, увеличенной в 3 раза, на рисунке 17.
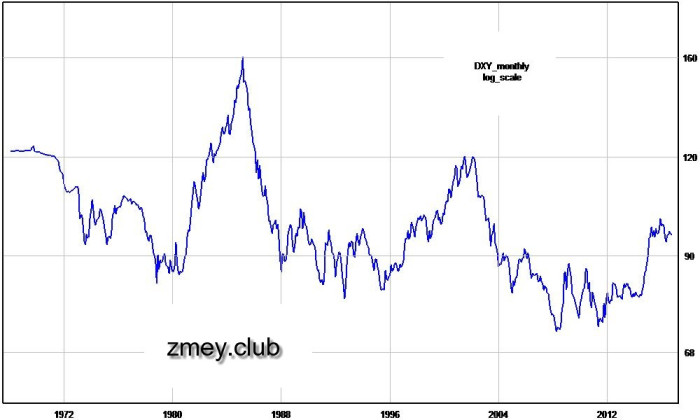
Рисунок 16 — исходный график индекса доллара.
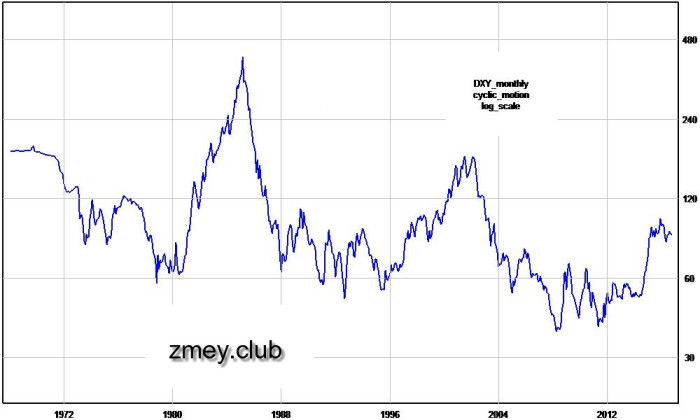
Рисунок 17 — график-аналог с расширенной амплитудой (d=100).
По золоту имеется другая проблема — долгосрочный восходящий тренд, который в данном случае нельзя ничем скомпенсировать, поскольку индекс доллара в силу особенностей ценообразования изначально развивается практически в горизонтальном канале. Разумеется, мы всегда можем использовать расчёты по чистому сентименту, но будет лучше если мы не станем накладывать одни предположения на другие и разделаемся с трендом каким-то иным способом, например, с помощью обычного дрейфа:
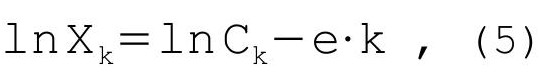
где k — порядковый номер бара, начиная с первого,
e — постоянная дрейфа (e>0).
Физически поправка на дрейф означает поворот графика по часовой стрелке вокруг бара с порядковым номером 0 — каждый последующий бар теряет в стоимости больше чем предыдущий, но все циклические пропорции при этом сохраняются. Величина е (в данном случае e=0.0054) подбирается таким образом, чтобы предполагаемые впадины в 1970-ом и в начале 2000-х годов находились чётко на одном уровне. Исходный график золота представлен на рисунке 18, а график с учётом дрейфа на рисунке 19.
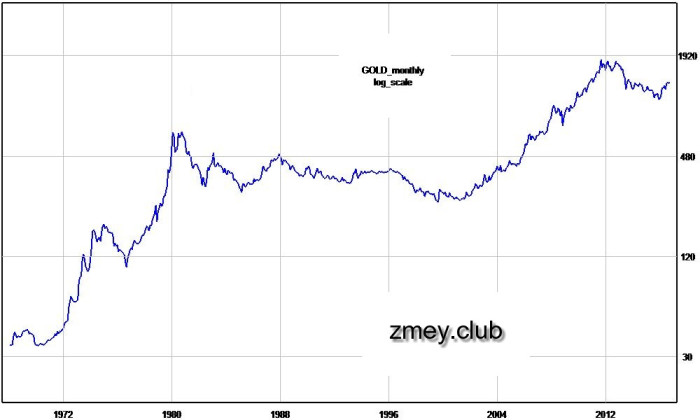
Рисунок 18 — исходный график по золоту.
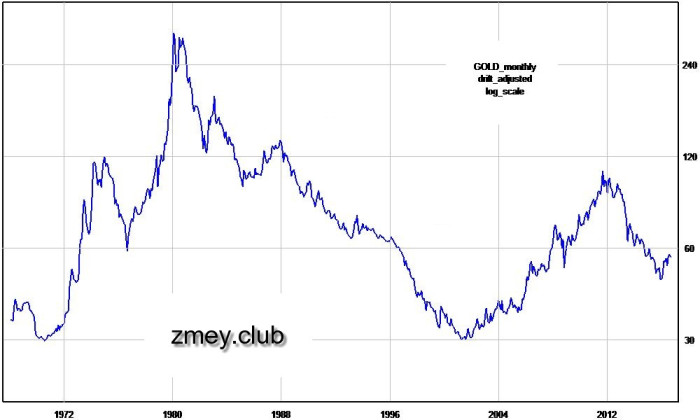
Рисунок 19 — график золота с поправкой на дрейф.
Правка на дрейф и вертикальное масштабирование по принципу паритета волатильностей это полный набор универсальных методов для приведения любого исходного графика к формализованному виду, то есть к горизонтальному каналу с наперёд заданной теоретической амплитудой. Вполне естественно, что подобные построения лишь отчасти отражают суть происходящего на финансовых рынках, но этим своим недостатком они практически не отличаются от исходного графика с номинальной ценой.
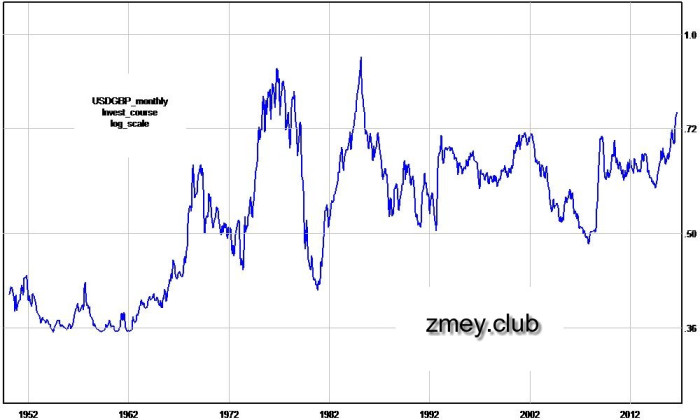
Рисунок 20 — график USDGBP (до 1979-го года — инвестиционный курс).
Из графика видно, что американская валюта относительно стерлинга росла с 1962-го по 1985-ый годы, а падала с 1985-го по 2008-ой. Получается, что глобально она ходит аккурат по циклам Кондратьева — против своего рынка и вместе с золотом. Проверим эту гипотезу, поочерёдно выполнив перемножение и деление приведённых котировок золота и индекса доллара. Результаты представлены на рисунках 21 и 22 соответственно. Графики нормированы, так что минимальные значения всегда равны единице.

Рисунок 21 — умножение приведённых котировок золота и индекса доллара.
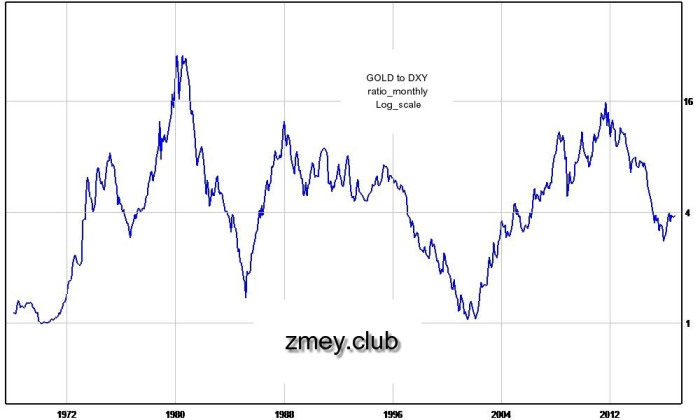
Рисунок 22 — отношение приведённых котировок золота и индекса доллара.
По-хорошему, время наблюдения недостаточно, но сделать основные выводы всё-таки можно — если все активы, действительно, имеют одинаковый характерный период, то доллар и золото определённо ходят вместе. Это единственное предположение, которое объясняет один большой цикл на первом графике и несколько маленьких на втором. Младшие циклы при этом торгуются явно в противофазе, о чём говорит отсутствие долгих коррекций на рисунке 21 и внушительная амплитуда на рисунке 22.
Такая двойственная картина имеет большой физический смысл. Локально золото ходит против доллара, потому что оно номинировано в американской валюте, так что её падение повышает привлекательность металла за пределами Соединённых Штатов. Глобально же, доллар и золото это две резервные валюты, которые втягивают капитал в условиях всеобщего страха и возвращают его, когда экономика переходит к стабильному росту. Без сомнения, золото это деньги!
Как сочетаются большие циклы по разным активам? Какие из них двигаются синхронно, а какие живут исключительно своей жизнью? Правда ли, что золото всегда ходит против доллара, а фондовой рынок США растёт только в условиях недорогой нефти? Как правильно формировать стратегический портфель и как выбирать для него действительно недооценённые активы? Как сравнить активы с принципиально разными свойствами и будет ли такое сравнение честным?
Когда аналитики говорят о сравнении, то обычно подразумевают корреляцию, если вообще используют какие-то научные методы. Для примера, коэффициент корреляции между золотом и индексом доллара за последние 20 лет составляет порядка -0.4 (на дневных данных) — этого явно мало для формирования портфеля «без риска», но вполне достаточно, чтобы эксперты видели в них полную противоположность. Следующий пример показывает насколько опасна такая концепция.
Рассмотрим два циклических ценовых ряда, построенных согласно принципам Хёрста:
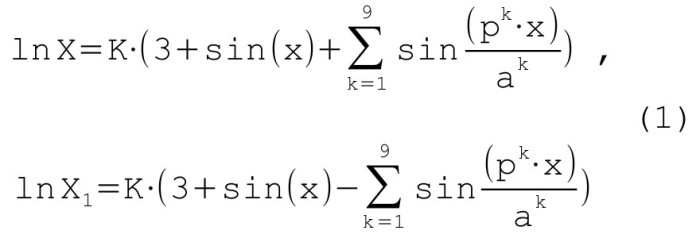
K=1, p=3.6, a=2
Как видно из формулы, слагаемые с наибольшим периодом софазны, тогда как все остальные торгуются чётко в противофазе. Периоды слагаемых попарно равны, а амплитуды снижаются вслед за периодом, хоть и не пропорциональны ему. Коэффициент корреляции в этой системе равен -0.98 (при разбиении интервала 0...2*Pi на 1000 элементарных отрезков), но это отнюдь не препятствие чтобы активы X и X1 глобально двигались вместе (рисунок 1), создавая ложное впечатление о своём характере.

Рисунок 1 — графики X и X1 (показано только три слагаемых ряда)
В дальнейшем я покажу, что описанная мной картина является только чересчур идеализированной, но отнюдь не чисто гипотетической, а это, в свою очередь, ставит под сомнение многие хорошо известные закономерности, а заодно и подрывает основы всей построенной на корреляциях портфельной теории, ведь по правилам математической логики одного-единственного негативного результата достаточно для отрицания всей концепции. Разумеется, теорию нужно дополнять, но никак не отбрасывать.
Амплитуда и волатильность.
Все активы, которые торгуются на финансовых рынках, немного разные. Они отличаются номинальной ценой, ожидаемой доходностью, а также принятой мерой риска — волатильностью: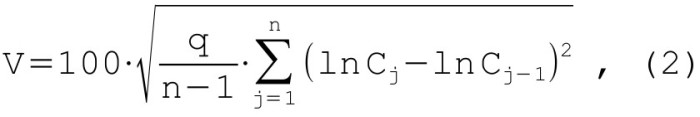
где Cj — цена закрытия рынка на баре с индексом j,
q — число наблюдений в году (для дневных данных q=252).
В традиционном понимании волатильность отвечает только за колебания рынка, но в действительности это интегральная характеристика, которая затрагивает и глобальные циклы, потому что все амплитуды обязательно связаны. Если одна из них отклонится от нормы, то на определённых тайм-фреймах станет выгодна систематическая игра или по тренду или против него, а это явное противоречие логике рынка, который не должен предоставлять трейдерам столь тривиальных возможностей.
Волатильность это объективная характеристика, которая, в отличии от всех амплитуд, рассчитывается непосредственно на основе ценовых данных с использованием простой и проверенной формулы. Кроме того, с графика чистого сентимента можно снять так называемую полную амплитуду А0, то есть разницу (в логарифмах) между вершиной и впадиной одного старшего цикла. Свяжем эти величины, используя их аналоги в рамках всё той же идеализированной циклической модели (формула 1):
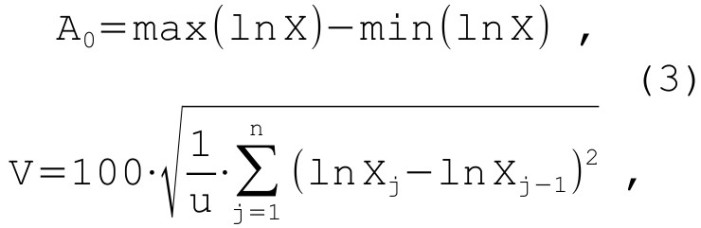
где u — период большого кондратьевского цикла.
Проведём численный эксперимент, чтобы установить, как именно те или иные переменные влияют на волатильность. Разобьём интервал 0...2*Pi на 10000 элементарных участков и зафиксируем значения p и a, после чего, варьируя коэффициентом K, будем добиваться изменения полной амплитуды. Построив график A0(V) (рисунок 2a) мы убедимся, что их взаимосвязь линейная (A0=U*V) и она остаётся таковой при любых значениях p и a, от которых зависит только лишь коэффициент U.

Рисунок 2a — взаимосвязь между волатильностью и полной амплитудой.
Рисунок 2b — взаимосвязь между амплитудой и периодом в идеальных циклах;
красная линия — экспериментальная, зелёная — приближение по формуле a=0.96+0.28p.
Значение коэффициента U=1/8 мы определим на основе реальных ценовых данных по шести наиболее ликвидным активам, предположив, что все они имеют одинаковый характерный период старшего цикла u=55 лет (таблица 1). Разброс полной амплитуды относительно её теоретического значения получается совсем небольшой, а это, в свою очередь, говорит не только об устойчивости найденного решения, но и также о фрактальном подобии графиков самых различных финансовых инструментов.

таблица 1 — волатильность и полная амплитуда по основным активам.
Напоследок мы решим обратную задачу, ради которой и затевался численный эксперимент — определим значения a и p, при которых коэффициент U = 1/8. Поскольку в нашей расчётной схеме неизвестных больше чем уравнений, то мы найдём только зависимость a(p), благо что она получается явной, то есть одному конкретному значению p соответствует одно конкретное значение a. Как видно из рисунка 2b, эта связь практически линейная, причём амплитуда убывает гораздо медленнее периода.
Теория сочетания циклов.
Рассмотрим две элементарные синусоидальные функции f1 и f2, периоды которых совпадают и равны 2 Pi (рисунок 3). Поскольку функции, по своей сути, являются логарифмом цены, то для их надлежащего сравнения нужно использовать разность f3=f1-f2 (рисунок 4) — на графике она будет полным аналогом от логарифма отношения котировок двух произвольных активов ln(A/B).
Рисунок 3 — исходные синусоидальные функции.
f1=3+sin(x),f2=3+sin(x+t).

Рисунок 4 — отношение функций с одинаковым периодом.
a — активы f1 и f2 торгуются в противофазе (t=Pi),
b — общий случай, когда фазы не совпадают.
Очевидно, что период результирующей функции при таком раскладе всегда будет равен периодам двух исходных за исключением одного-единственного случая (t=0), когда f3 вырождается в прямую линию. Амплитуда f3 также зависит от величины t, достигая своего пика в противофазе (t=Pi). Циклы итоговой функции симметричны относительно вертикалей, проведённых через вершины, фаза равна -t/2.
Теперь усложним картину и представим, что каждая исходная функция является суммой двух синусоид, младшая из которых имеет реалистичную амплитуду, соразмерную своему периоду (рисунок 5).

Рисунок 5 — исходные функции, состоящие из двух синусоид.
f1=3+sin(x)+sin(px)/a; f2=3+sin(x+t1)+sin(px+t2)/a.

Рисунок 6 — отношение функций, состоящих из двух синусоид.
Параметры расчёта: p=3.6, a=2, t1=Pi/2, t2=Pi/3.
Как видно из рисунка 6, характерный период результирующей функции f3 по-прежнему равен 2*Pi, то есть глобальная циклическая картина определяется соотношением только первых слагаемых исходных функций, имеющих наибольшую амплитуду. Все остальные компоненты f1 и f2 влияют только на форму результирующей функции. Если младшие циклы находятся в противофазе, тогда перепады настроения на графике f3 получатся особенно резкими. Софазные младшие циклы взаимно уничтожаются.
Следующий пример, когда периоды старших циклов несколько отличаются, но их амплитуды абсолютно равны (рисунок 7). Периоды младших циклов пропорциональны старшим, фазы не имеют значения.

Рисунок 7 — исходные функции с разными периодами.
f1=3+sin(x)+sin(px)/a; f2=3+sin(qx)+sin(qpx+t)/a.

Рисунок 8 — отношение функций с разными периодами.
Параметры расчёта: p=3.6, a=2, q=3/4, t=Pi/2.
Рисунок 8 наглядно показывает что происходит с результирующей функцией f3, если исходные активы не связаны никакими взаимными обязательствами. В одной части графика может наблюдаться широкий диапазон с метаниями из стороны в сторону, но за ним неизбежно последуют несколько острых циклов, когда глобальные низы по одному активу начнут совпадать с верхами другого. Картинка при этом будет очень похожа на случай равных периодов в противофазе, но это не продлится долго.

Рисунок 9 — исходные функции (старшие циклы софазны).
f1=3+sin(x)+sin(px)/a; f2=3+sin(x+t1)+sin(px+t2)/a.
Последняя реалистичная ситуация, когда старшие циклы исходных функций имеют равный период, но их фазы практически совпадают (рисунок 9). При вычитании подобные циклы взаимно уничтожаются, оставляя после себя колебания с периодом 2*Pi/p (рисунок 10), зато при сложении они отлично видны (рисунок 11). Средний период по-прежнему равен 2*Pi, а вот полная амплитуда, если младшие циклы в противофазе, может оказаться практически равной амплитуде на рисунке 10.

Рисунок 10 — вычитание функций (старшие циклы софазны)
Параметры расчёта: p=3.6, a=2, t1=Pi/6, t2=-3*Pi/4.

Рисунок 11 — сложение функций (старшие циклы софазны).
Параметры расчёта: p=3.6, a=2, t1=Pi/6, t2=-3*Pi/4.
Очевидно, что полная независимость каких-то активов это чисто гипотетический случай, потому что все они связаны через инфляцию, которая является такой же циклической функцией. Нам должно выбрать — либо все активы имеют одинаковый характерный период, равный периоду цикла Кондратьева, либо в один прекрасный момент на пике инфляции мы получим низкие процентные ставки, недорогое сырьё и пузырь на фондовом рынке. Логика ценообразования подсказывает, что выбирать нужно первое.
Получается, что всё многообразие вариантов, по сути, сводится только к рассмотрению фазы. При этом, имея даже сравнительно небольшую историю (примерно 60 лет), на основе результирующей функции можно однозначно определить все свойства исходных. Если периодично соотношение котировок, тогда исходные активы имеют разную фазу, если периодично произведение, тогда фазы должны совпадать. Таким образом, для выявления циклических свойств не нужно делать никаких вычислений!
Нефть, золото и индекс SP500.
Как ясно следует из теории, анализ сочетаемости циклов должно проводить на основе ценовых данных, очищенных от инфляции и всех остальных факторов роста. Впрочем, для подтверждения самой теории можно взять и обычные котировки — если действие указанных факторов консервативно и одновременно приводит к росту обоих активов, которые мы наблюдаем, то их отношение окажется вполне нормальной циклической функцией, пускай даже и сильно выходящей за пределы горизонтального канала.
Рисунок 12 — отношение индекса S&P500 к золоту.
На рисунке 12 показано отношение индекса S&P500 к золоту — периодическая картина здесь аккуратно повторяет циклы Кондратьева по самому рынку Соединённых Штатов, а глобальные волны не содержат никакого постороннего шума. Нет сомнений, что эти активы циклически связаны, причём торгуются они практически в противофазе. Старшие верхи по индексу S&P совпадают с низами по золоту и наоборот; по времени разница между точками разворота составляет не больше 5 лет.
Безусловно, твёрдые котировки золота до начала 70-х годов наложили свой отпечаток на график, но их влияние лучше всего заметно как раз там, где циклическая картина содержит какие-то искажения — это болтанка 33-го года и слишком мелкая впадина в начале 40-х. Ранее 1920-го года наш график и вовсе не показателен, поскольку индекс S&P в те времена никак не отражал динамику капитализации рынка. Это тот случай, когда влияние факторов роста нельзя считать консервативным.

Рисунок 13 — отношение индекса S&P500 к нефти.
На рисунке 13 показано отношение индекса S&P500 к нефти — и циклы здесь тоже видны. Они не столь безупречны в плане шума, но такая картина указывает лишь на различную природу ценообразования. Для золота, валюты и фондовых рынков фактором роста является денежная масса, для нефти — только инфляция. Эти величины связаны между собой циклически, но никакой функциональной зависимости между ними, разумеется, нет — это и приводит к «потрясениям» на графике.
Сравнение чистых сентиментов (рисунок 14) позволяет нам получить более совершенную циклическую картину. Как и положено, график теперь развивается в горизонтальном канале, а чрезмерный рост с 2014-го года отлично укладывается в рамки коррекции, необходимой для растягивания цикла вправо. Волатильность нефти и наличие длительных периодов дисбаланса спроса и предложения по-прежнему напоминают о себе, но положения главных вершин и впадин они не меняют.

Рисунок 14 — отношение рынка акций США к нефти (чистый сентимент).
На протяжении всего XX века ключевые низы по американскому рынку с точностью до нескольких лет совпадали с верхами по нефти, если считать их в постоянных долларах — так было в 1921-ом, 1949-ом, 1982-ом и 2008-ом годах. При этом на истории хватает примеров, когда нефть и фондовый рынок США годами уверенно двигались в одну сторону, но это случалось исключительно по вине младших циклов, которые в случае с нефтью имеют запредельную и нестабильную амплитуду.
Годы Великой Депрессии проясняют нам некоторые особенности ценообразования нефти и золота. Так, падение рынка с 1929-го по 1932-ой годы проходило в условиях резкого увеличения спроса на золото, что в итоге привело к повышению его официального курса, тогда как нефть, следуя в русле дефляции, продолжала своё падение вплоть до 1933-го года. Тем не менее, к 1949-му году, когда американский рынок достиг существенной впадины, нефть догнала золото и также установила вершину.

Рисунок 15 — отношение золота к нефти.
Отдельно отмечу, что исследование циклических свойств требует особой тщательности и всестороннего анализа фактов. Так, рассматривая график отношения золота к нефти (рисунок 15) мы запросто могли обмануться, предположив их разную периодичность. Картина прояснилась только при их сравнении с индексом S&P500 — несмотря на различную природу факторов роста глобально нефть и золото всё-таки ходят вместе, как того требует логика инфляционных циклов.
Дрейф и паритет волатильностей.
При постановке численных экспериментов я сознательно использовал циклы с равными амплитудами, ибо в противном случае наиболее волатильный актив просто подавляет движения своего оппонента, не давая тому ни единого шанса проявить себя на графике отношения. Небольшая разница в амплитудах, как в случае золота и индекса S&P, позволяет пренебречь ею, но в ситуации, когда противником золота выступает индекс доллара или другой неторопливый актив, такой подход уже не работает.По сути, наша задача заключается в том, чтобы придумать аналог исходного графика, на котором будут сохранены все базовые пропорции, но волатильность и, как следствие, полная амплитуда цикла станут равными соответствующим показателям другого актива. Логически это означает, что разницы котировок между двумя произвольными барами на основном графике и на его аналоге всегда отличаются ровно в u раз. Отсюда, массив данных для построения графика-аналога определяется формулой:
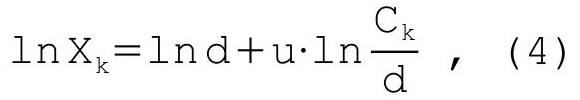
где Сk — исходная котировка на баре с индексом k,
d — любое положительное число (d>0).
Коэффициент u равен отношению волатильностей двух сопоставляемых активов, так что весь принцип, согласно которому один из них растягивается по вертикали, можно смело назвать паритетом величины V. Параметр d в данном случае просто число, прибавленное к функции, — оно определяет номинальную котировку, но никак не влияет на логарифмические пропорции. Исходный график по индексу доллара представлен на рисунке 16, а его аналог с амплитудой, увеличенной в 3 раза, на рисунке 17.

Рисунок 16 — исходный график индекса доллара.

Рисунок 17 — график-аналог с расширенной амплитудой (d=100).
По золоту имеется другая проблема — долгосрочный восходящий тренд, который в данном случае нельзя ничем скомпенсировать, поскольку индекс доллара в силу особенностей ценообразования изначально развивается практически в горизонтальном канале. Разумеется, мы всегда можем использовать расчёты по чистому сентименту, но будет лучше если мы не станем накладывать одни предположения на другие и разделаемся с трендом каким-то иным способом, например, с помощью обычного дрейфа:
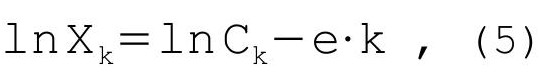
где k — порядковый номер бара, начиная с первого,
e — постоянная дрейфа (e>0).
Физически поправка на дрейф означает поворот графика по часовой стрелке вокруг бара с порядковым номером 0 — каждый последующий бар теряет в стоимости больше чем предыдущий, но все циклические пропорции при этом сохраняются. Величина е (в данном случае e=0.0054) подбирается таким образом, чтобы предполагаемые впадины в 1970-ом и в начале 2000-х годов находились чётко на одном уровне. Исходный график золота представлен на рисунке 18, а график с учётом дрейфа на рисунке 19.

Рисунок 18 — исходный график по золоту.

Рисунок 19 — график золота с поправкой на дрейф.
Правка на дрейф и вертикальное масштабирование по принципу паритета волатильностей это полный набор универсальных методов для приведения любого исходного графика к формализованному виду, то есть к горизонтальному каналу с наперёд заданной теоретической амплитудой. Вполне естественно, что подобные построения лишь отчасти отражают суть происходящего на финансовых рынках, но этим своим недостатком они практически не отличаются от исходного графика с номинальной ценой.
Доллар и золото.
Обратимся к истории, чтобы понять как именно доллар и золото связаны между собой. Формально в 70-е годы индекс доллара пребывал в нисходящем канале, но это движение с точки зрения циклов нельзя считать показательным, поскольку валютные курсы только переходили к рыночному ценообразованию. Реальная картина хоть немного проявляется только на графике USDGBP (рисунок 20), в котором учтён параллельный инвестиционный курс, существовавший в Британии с 1950-го по 1979-ый годы.
Рисунок 20 — график USDGBP (до 1979-го года — инвестиционный курс).
Из графика видно, что американская валюта относительно стерлинга росла с 1962-го по 1985-ый годы, а падала с 1985-го по 2008-ой. Получается, что глобально она ходит аккурат по циклам Кондратьева — против своего рынка и вместе с золотом. Проверим эту гипотезу, поочерёдно выполнив перемножение и деление приведённых котировок золота и индекса доллара. Результаты представлены на рисунках 21 и 22 соответственно. Графики нормированы, так что минимальные значения всегда равны единице.

Рисунок 21 — умножение приведённых котировок золота и индекса доллара.

Рисунок 22 — отношение приведённых котировок золота и индекса доллара.
По-хорошему, время наблюдения недостаточно, но сделать основные выводы всё-таки можно — если все активы, действительно, имеют одинаковый характерный период, то доллар и золото определённо ходят вместе. Это единственное предположение, которое объясняет один большой цикл на первом графике и несколько маленьких на втором. Младшие циклы при этом торгуются явно в противофазе, о чём говорит отсутствие долгих коррекций на рисунке 21 и внушительная амплитуда на рисунке 22.
Такая двойственная картина имеет большой физический смысл. Локально золото ходит против доллара, потому что оно номинировано в американской валюте, так что её падение повышает привлекательность металла за пределами Соединённых Штатов. Глобально же, доллар и золото это две резервные валюты, которые втягивают капитал в условиях всеобщего страха и возвращают его, когда экономика переходит к стабильному росту. Без сомнения, золото это деньги!

8 комментариев
Сергей, насколько этими неизвестными можно пренебречь, исследовал ли ты их влияние? Или это только предположение?
— очень похоже на научное обоснование 1/2.
Насчёт 1/2 я не понял. Поясни.
2. 1/2 Это условная точка вращения «0». Расстояние от А до 0, которое уже цена прошла, равно предполагаемому движению от 0 до Б